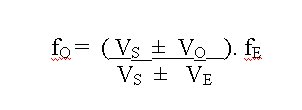¿Son absolutas las frecuencias sonoras?
Decimos que una magnitud es absoluta cuando medida desde diferentes sistemas de referencia obtenemos exactamente el mismo valor. Pues bien, la frecuencia de un sonido no es una magnitud absoluta sino relativa, como demostró teóricamente el físico austríaco Christian Doppler en 1842. Doppler observó que si la fuente emisora de sonido o el receptor se encuentran en movimiento uno respecto al otro, la frecuencia se mide diferente a que si se hallan en reposo. Una serie de experimentos realizados en 1845 por el físico francés Ballot demostraron el acierto de las predicciones de Doppler. El experimento exigía que una locomotora tirase de un vagón plataforma sobre el cual tocaba una banda de trompetistas; cuando dicho tren se acercaba y alejaba de la estación donde se hallaban los observadores, los mismos lograron medir las diferencias de frecuencia mencionadas.
Hoy día, los cambios de frecuencia debidos al movimiento –y hablamos a veces de movimientos que implican desplazamientos sumamente pequeños- no solamente en el caso de las ondas sonoras, sino también para la luz y otras ondas electromagnéticas, son la base de numerosas aplicaciones tecnológicas: los radares detectores de velocidad usados por la Policía, la detección de huracanes, la medición de la velocidad del flujo sanguíneo de los pacientes, la visualización de los latidos del corazón de un feto en el seno de su madre, la medición de la velocidad de una estrella...
¿En qué consiste concretamente el efecto Doppler?
I. VIENDO EL EFECTO DOPPLER
(1) Considera una fuente o emisor de ondas circulares, inicialmente en reposo.
Las ondas emitidas tendrán esta forma:
En todas las direcciones, la distancia entre las crestas de las ondas es similar, por lo tanto la longitud de onda y la frecuencia son constantes. Un observador quieto respecto al emisor mdirá la misma frecuencia independientemente del lugar en que se halle.
(2) Digamos que ahora el emisor se mueve hacia la izquierda con una velocidad de 136m/s respecto a tierra y que la velocidad del sonido vale 340m/s. El aspecto de las ondas ahora será el siguiente:
Puedes observar como las ondas se "amontonan" a la izquierda y se "separan" a la derecha. Un observador ubicado a la izquierda de la fuente mediría una frecuencia MAYOR, ya que la longitud de onda disminuye. Otro observador, situado a la derecha de la fuente mediría una frecuencia MENOR, ya que la longitud de onda aumenta.
(3) A medida que la velocidad de la fuente se incrementa, el efecto se vuelve más notorio.
(4) Si la velocidad del emisor es mayor que la velocidad del sonido se observa esto
El emisor deja atrás las ondas, y la tangente a las mismas forma un frente plano llamado "onda de choque". Esto ocurre con aquellos aviones que rompen la barrera del sonido. Esa onda de choque genera un estallido sónico muy notorio.
La onda de choque no solamente aparece en el caso del sonido: una lancha que de desplaza por aguas tranquilas a mayor velocidad que la que se pueden mover las ondas en el agua también crea en su proa una onda de choque, que tiene una característica forma de "V"
II. LA FRECUENCIA RELATIVA
Se puede demostrar matemáticamente que la frecuencia que percibe un observador no será en general igual a la frecuencia con que emite la fuente, ya que esto no solamente depende del movimiento de la fuente sino del movimiento del observador (recuerda que el concepto de movimiento es relativo).
La expresión matemática del Efecto Doppler es la siguiente:
siendo:
fO la frecuencia del sonido percibida por el observador,
fE la frecuencia del sonido emitida por la fuente o emisor,
VS la velocidad del sonido,
VO la velocidad con que se mueve el observador respecto a tierra y
VE la velocidad con que se mueve el emisor respecto a tierra.
Observa que en la ecuación aparece dos veces el signo "±". Esto es debido a que las fercuencia percibida depende no solamente de que el observador y el emisor se muevan, sino también de hacia adónde se mueven. Para saber cuándo se debe usar uno u otro signo se usan dos reglas sencillas:
Regla 1: El sentido positivo de las velocidades será aquel en el que debe moverse el
observador para acercarse a la fuente.
Regla 2: El signo de VS se considera siempre positivo.
III. JUGANDO CON EL EFECTO DOPPLER
Tu mismo puedes ver el efecto Doppler en acción, cambiando la relación entre la velocidad de la fuente (V) y la velocidad del sonido (VS) utilizando la Applet Java de W. Bauer en esta dirección de Internet.
Simplemente, haz un click sobre la pantalla gris y arrastra el mouse con el botón izquierdo apretado hacia donde quieras que se mueva el objeto. Cuanto más lo arrastres, mayor será la relación V/VS .